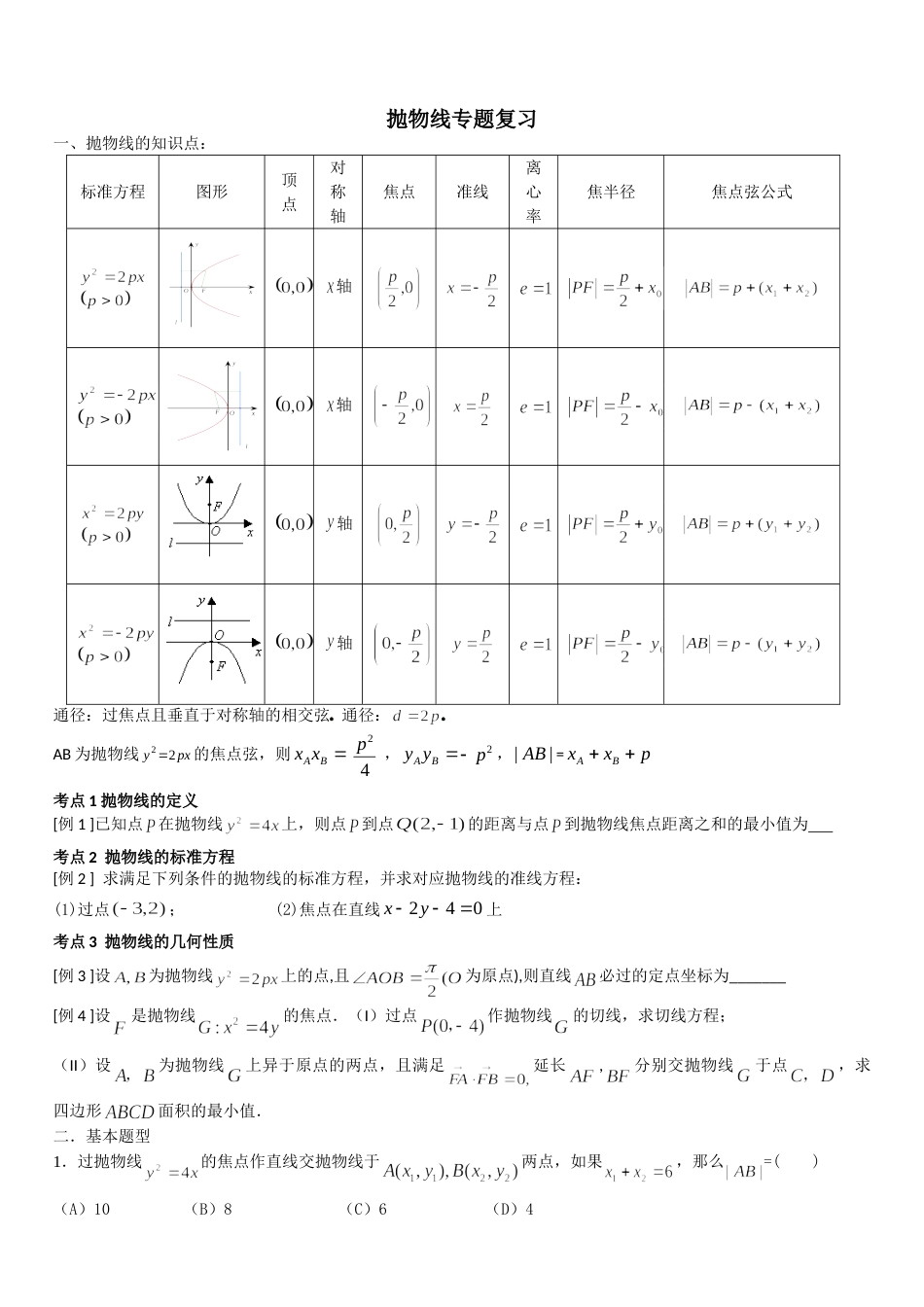
抛物线专题复习一、抛物线的知识点：标准方程图形顶点对称轴焦点准线离心率焦半径焦点弦公式轴轴轴轴通径：过焦点且垂直于对称轴的相交弦奎屯王新敞新疆通径：奎屯王新敞新疆AB为抛物线pxy22的焦点弦，则xAxB4p2，yAyBp2，||AB=pxxBA考点1抛物线的定义[例1]已知点在抛物线上，则点到点的距离与点到抛物线焦点距离之和的最小值为考点2抛物线的标准方程[例2]求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：(1)过点；(2)焦点在直线240xy上考点3抛物线的几何性质[例3]设为抛物线上的点,且为原点),则直线必过的定点坐标为_______[例4]设是抛物线的焦点．（I）过点作抛物线的切线，求切线方程；（II）设为抛物线上异于原点的两点，且满足延长,分别交抛物线于点，求四边形面积的最小值．二．基本题型1．过抛物线的焦点作直线交抛物线于两点，如果，那么=()（A）10（B）8（C）6（D）42．已知抛物线22(0)ypxp的焦点为F，点111222()()PxyPxy，，，，333()Px，y在抛物线上，且||1FP、||2FP、||3FP成等差数列，则有（）A．321xxxB．321yyyC．2312xxxD.2312yyy3．已知为抛物线上一动点，为抛物线的焦点，定点，则的最小值为（）（A）3（B）4（C）5（D）64．过抛物线的焦点作直线交抛物线于、两点，则（）（A）（B）（C）（D）5．已知抛物线C：的焦点为准线为过抛物线C上的点A作准线l的垂线，垂足为M，若△AMF与△AOF(其中O为坐标原点)的面积之比为3：1，则点A的坐标为()A．(2,2)B．(2，－2)C．(2，±)D．(2，±2)6．过抛物线焦点F的直线与抛物线交于两点A、B,若A、B在抛物线准线上的射影为A1,B1,则A1FB1（）A.45B.60C.90D.1207．两个正数a、b的等差中项是92，一个等比中项是25，且a,b则抛物线2()ybax的焦点坐标为（）A．1(0,4)B．1(0,)4C．(12,0)D．(14,0)8．抛物线,42Fxy的焦点为准线为与轴相交于点过且倾斜角等于的直线与抛物线在轴上方的部分相交于点垂足为则四边形的面积等于（）A．33B．43C．63D．389．已知抛物线C：,过点和点的直线与抛物线C没有公共点，则实数t的取值范围是()A．B.C．D．10．如果1P，2P，…，8P是抛物线24yx上的点，它们的横坐标依次为1x，2x，…，8x，F是抛物线的焦点，若)(,,,21xnNxxn成等差数列且45921xxx，则||5FP=（）．A．5B．6C．7D．911．设O是坐标原点，F是抛物线24yx的焦点，A是抛物线上的一点，FA�与x轴正向的夹角为60，则OA�为．12．若直线10axy经过抛物线24yx的焦点，则实数a13．若抛物线22ypx的焦点与双曲线2213xy的右焦点重合,则p的值14．(文)如图，过抛物线y2＝2px(p>0)的焦点F作倾斜角为60°的直线l，交抛物线于A、B两点，且|FA|＝3，则抛物线的方程是________．15．抛物线的顶点在原点,开口向上,为焦点为准线与轴的交点为抛物线上一点,且|317|,||AFAM，求此抛物线的方程．16．在抛物线42yx上求一点，使该点到直线45yx的距离为最短，求该点的坐标．17．设抛物线22ypx(p0)的焦点为经过点的直线交抛物线于两点．点在抛物线的准线上，且∥轴．证明直线经过原点．18．已知直线与抛物线相交于、两点，若，（为坐标原点）且，求抛物线的方程．19．椭圆12222byax上有一点在抛物线pxy22（p>0）的准线上，抛物线的焦点也是椭圆焦点.（1）求椭圆方程；（2）若点在抛物线上，过作准线的垂线，垂足为距离，求的最小值.20．椭圆C1：＜＜的离心率抛物线C2：＞的焦点在椭圆C1的顶点上．(1)求抛物线C2的方程；(2)若过的直线与抛物线C2交于E、F两点，又过E、F作抛物线C2的切线l1、l2，当l1⊥l2时，求直线的方程．21．已知抛物线C：的焦点为过点的直线l与C相交于A、B两点，点A关于x轴的对称点为D.(1)证明：，点在直线上；(2)设求的内切圆的方程．20．(文)[解析](1)已知椭圆的长半轴长为a＝2，半焦距c＝，由离心率e＝＝＝得，b2＝1.∴椭圆的上顶点为(0,1)，即抛物线的焦点为(0,1)，∴p＝2，抛物线的方程为x2＝4y.(2)由题知直线l的斜率存在且不为零，则可设直线l的方程为y＝k(x＋1)，E(x1，y1)，F(x2，y2)， y＝x2，∴y′＝...