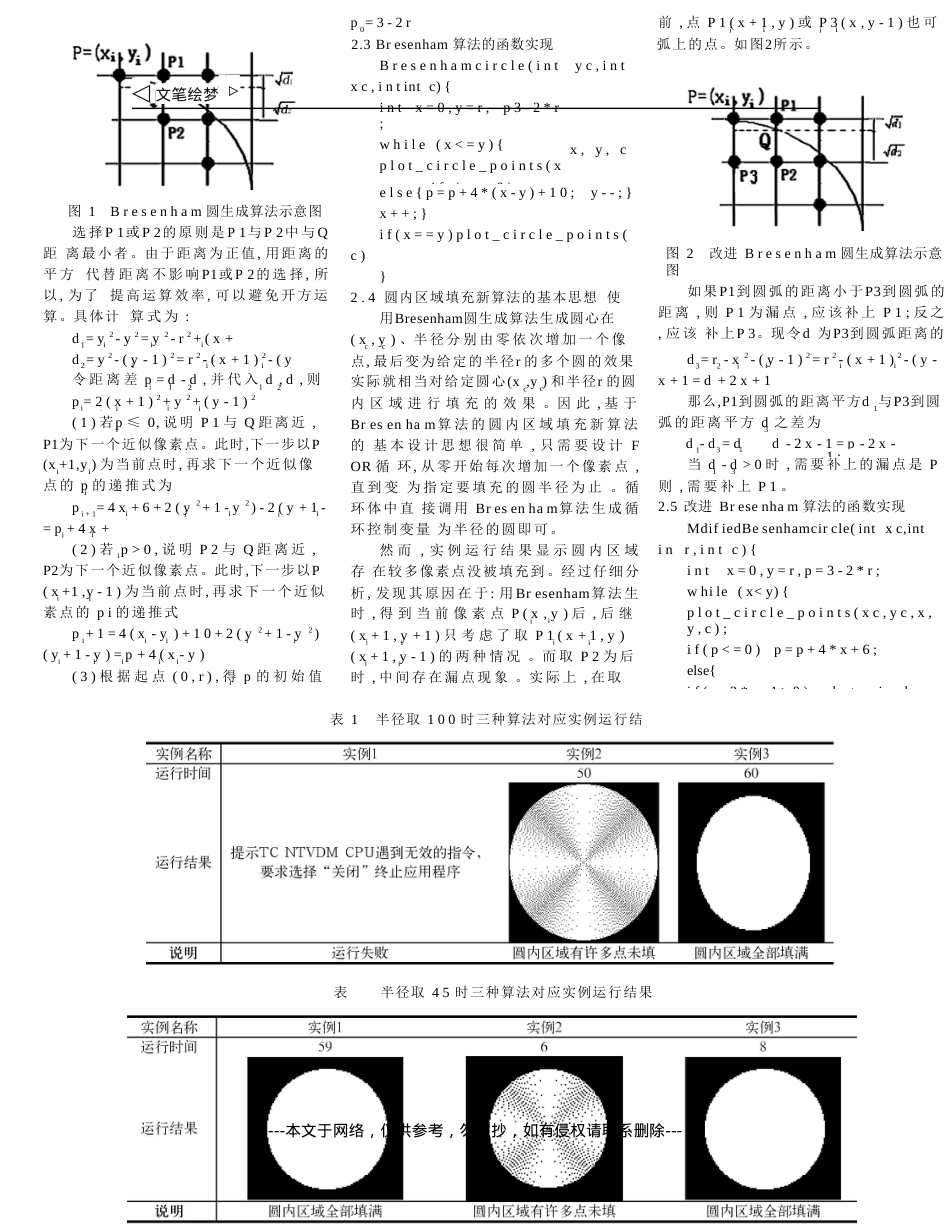
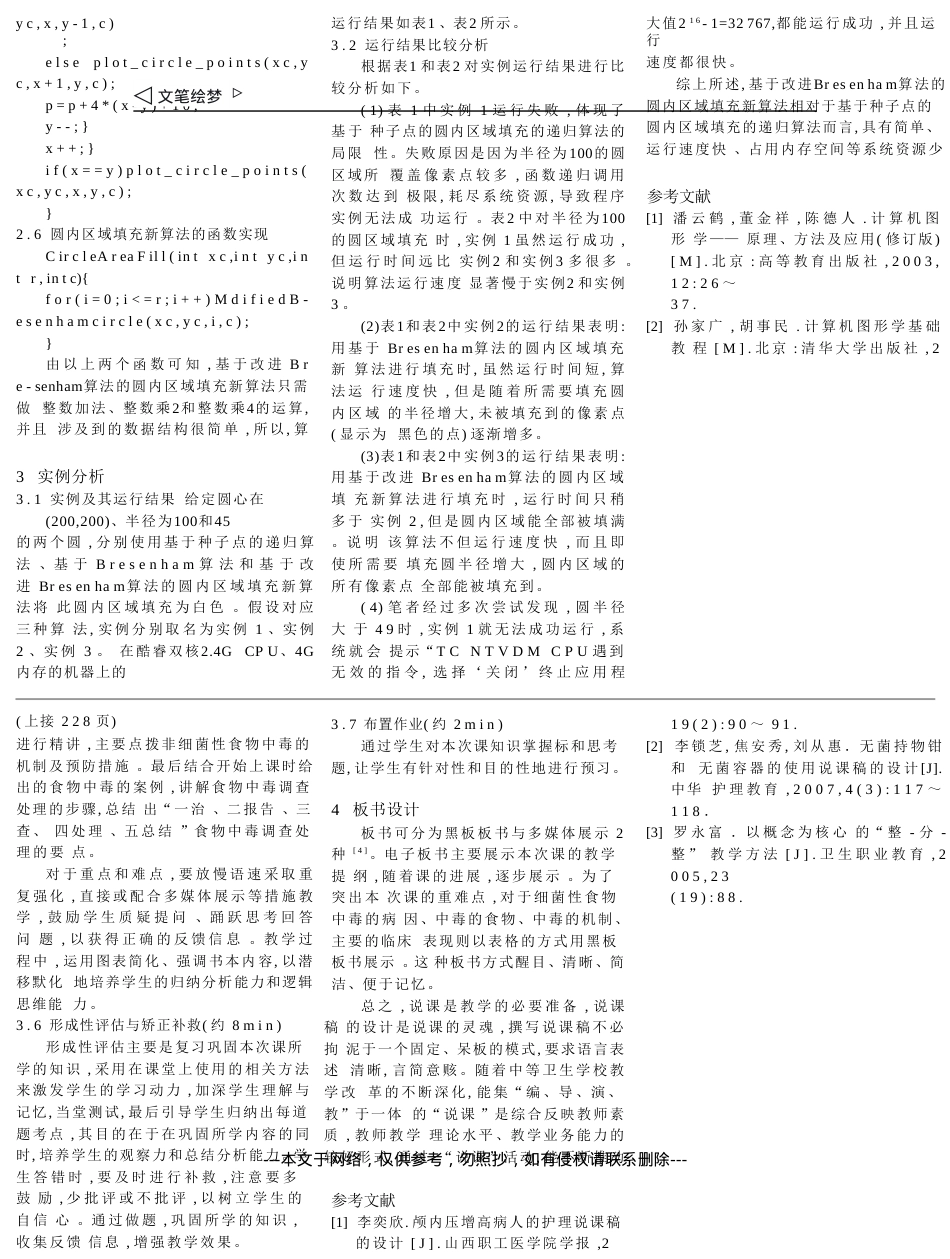
一种基于Bresenham算法的圆内区域填充新算法莫礼平唐安摘要:为了克服计算机图形学中的基于种子点的圆内区域填充的递归算法的不足,提出了一种基于改进的Bresenham圆生成算法的非递归的圆内区域填充新算法。实例证明,相对递归填充算法,新算法具有简单、快速、精确且占用内存空间小的优点。关键词:计算机图形学圆区域填充Bresenham算法:G642文献标识码:A:1672-3791(2009)11(c)-0229-03计算机图形学是研究如何用计算机生成、处理和显示图形的一门学科[1-2]。随着计算机图形学的不断发展,其应用范围日趋广泛。在计算机显示器屏幕上生成的任何图形都是像素点的集合。圆内区域填充的过程实质上就是寻找最佳逼近给定圆心和半径的圆周范围内的像素点序列,并向图形卡帧缓存器的相应单元填入颜色数据的过程。作为最低层的计算机图形、图像处理算法,圆内区域填充算法大量应用于计算机辅助设计与制造、计算机软件用户接口、计算机动画和艺术等领域。因此,对圆内区域填充算法进行研究,有着非常重要的意义。假设(x,y)为圆内区域内的一点,oldcolor为圆内区域填充前的颜色,需将整个圆内区域填充为新颜色newcolor。内点表示的四连通区域的递归填充算法的实现函数如下:置和管理系统堆栈。每调用一次递归函数就“入栈”一次,函数执行完一次,结果就“出栈”一次。圆内区域填充的递归算法函数的递归调用次数由需要填充的像素点数目决定。所需要填充的区域越广,所覆盖像素点越多,函数递归调用次数就越多,系统“入栈”和“出栈”操作越多,所消耗的内存空间等系统资源越多,执行时间就越长。当递归调用次数达到一定数目时,就会耗尽系统资源,导致应用程序无法运行。实际应用中,对圆内区域进行填充时,所覆盖的像素点数目一般至少是成百上千、甚至是成千上万的。因此,用基于种子点的圆内区域填充的递归算法填充时,不但速度慢,而且还有可能导致程序无法运行、填充任务无法完成的情况发生。因此,基于种子点的圆内区域填充的递归算法的应用只局限于需要intInnerPointFill4(intoldcolor,intnewcolor){x,inty,intif(getpixel(x,y)==oldcolor){putpixel(x,y,newcolor);InnerPointFill4(x,y+1,oldcolor,newcolor);InnerPointFill4(x,y-1,oldcolor,newcolor);InnerPointFill4(x-1,y,oldcolor,newcolor);InnerPointFill4(x+1,y,oldcolor,newcolor);}}1.2.2边界表示的四连通区域的递归填充算法假设(x,y)为圆内区域内部的一点,boundarycolor为原圆内区域边界的颜色,需要将整个圆内区域填充为新的颜色newcolor,则可以构造边界表示的四连通区域的递归填充算法的实现函数如下:1基于种子点的圆内区域填充的递归算法1.1算法的基本思想[1-2]基于种子点的圆内区域填充的递归算法是比较经典的算法。其基本思想是:先将圆内区域的一点赋予指定的颜色,然后将该颜色递归地扩展到整个圆内区域。该算法要求区域是四连通区域和八连通区域。即要求从区域上一点出发,通过上下左右4个方向的移动组合或上下左右、左上、右上、左下、右下8个方向的移动组合,在不越出区域的前提下,能到达区域内的任意像素点。圆内区域可用内点(圆内区域的像素点)表示或边界(圆周线上的像素点)表示。因此,基于种子点的圆内区域填充的递归算法对当前点是否需要进行递归填充的判断标准有两种:一是当前点是旧颜色的内点,则对它进行递归填充;二是当前点既非已填充为新颜色的内点也非边界点,则对它进行递归填充。基于种子点的圆内区域填充的递归算法可以分为四种:内点表示的四连通区域递归填充算法、内点表示的八连通区域递归填充算法、边界表示的四连通区域递归填充算法、边界表示的八连通区域递归填充算法。由于八连通区域的递归填充算法过程非常缓慢,且有可能出现所填像素点出界的现象[2],所以,实际常用四连通区域的两种递归填充算法。1.2算法的函数实现1.2.1内点表示的四连通区域的递归填充算法2基于改进的Bresenham圆生成算法的圆内区域填充新算法2.1圆的八对称性圆心位于原点的圆有四条对称轴x=0,y=0,x=y和x=-y。如果已知圆心在(x,y)cc的圆弧上一点(x,y),可以得到该点关于上voidBoundaryFill4(intx,intboundarycolor,intnewcolor){y,int述四条对称轴的其它7个点(x+...